Question 44 | JAMB Maths Objective 2024

Question: Find ∫(sinx+2)dx

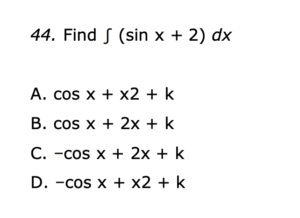
Step 1: Understand the Problem

We are being asked to integrate the function sin(x) + 2. This means we want to find a function whose derivative is sin(x) + 2.

Step 2: Split the Integral

We can rewrite the problem as:
∫(sin(x) + 2) dx = ∫sin(x) dx + ∫2 dx
This is because the integral of a sum is the sum of the integrals.

Step 3: Solve Each Part

1. Find ∫sin(x) dx:
   – The integral of sin(x) is -cos(x). (This is because the derivative of -cos(x) is sin(x).)
   – So, ∫sin(x) dx = -cos(x).
2. Find ∫2 dx:
   – The integral of a constant, like 2, is 2x. (This is because the derivative of 2x is 2.)
   – So, ∫2 dx = 2x.

Step 4: Add the Results

Now, combine the two results:
∫(sin(x) + 2) dx = -cos(x) + 2x + C
Here, C is the constant of integration, which we always add when finding indefinite integrals.

Step 5: Match with the Choices

Looking at the options:
– A: cos(x) + x2 + k → Incorrect because it has cos(x) instead of -cos(x).
– B: cos(x) + 2x + k → Incorrect because it has cos(x) instead of -cos(x).
– C: -cos(x) + 2x + k → Correct because it matches our result.
– D: -cos(x) + x2 + k → Incorrect because it has x2 instead of 2x.

Final Answer:

C. -cos(x) + 2x + k